ec89c4efc300b7e3e5622c6cd018d6fe7deda55b,GPy/inference/EP.py,DTC,fit_EP,#DTC#,133
Before Change
sigma_ = 1./tau_
mu_ = v_/tau_
self.tau_ = np.empty(self.N,dtype=float)
self.v_ = np.empty(self.N,dtype=float)
//Initial values - Marginal moments
z = np.empty(self.N,dtype=float)
self.Z_hat = np.empty(self.N,dtype=float)
phi = np.empty(self.N,dtype=float)
mu_hat = np.empty(self.N,dtype=float)
sigma2_hat = np.empty(self.N,dtype=float)
//Approximation
epsilon_np1 = 1
epsilon_np2 = 1
self.iterations = 0
self.np1 = [self.tau_tilde.copy()]
self.np2 = [self.v_tilde.copy()]
while epsilon_np1 > self.epsilon or epsilon_np2 > self.epsilon:
update_order = np.arange(self.N)
random.shuffle(update_order)
for i in update_order:
//Cavity distribution parameters
self.tau_[i] = 1./self.Sigma_diag[i] - self.eta*self.tau_tilde[i]
self.v_[i] = self.mu[i]/self.Sigma_diag[i] - self.eta*self.v_tilde[i]
//Marginal moments
self.Z_hat[i], mu_hat[i], sigma2_hat[i] = self.likelihood.moments_match(i,self.tau_[i],self.v_[i])
//Site parameters update
Delta_tau = self.delta/self.eta*(1./sigma2_hat[i] - 1./self.Sigma_diag[i])
Delta_v = self.delta/self.eta*(mu_hat[i]/sigma2_hat[i] - self.mu[i]/self.Sigma_diag[i])
self.tau_tilde[i] = self.tau_tilde[i] + Delta_tau
self.v_tilde[i] = self.v_tilde[i] + Delta_v
//Posterior distribution parameters update
self.LLT = self.LLT + np.outer(self.Kmn[:,i],self.Kmn[:,i])*Delta_tau
L = jitchol(self.LLT)
V,info = linalg.flapack.dtrtrs(L,self.Kmn,lower=1)
self.Sigma_diag = np.sum(V*V,-2)
si = np.sum(V.T*V[:,i],-1)
self.mu = self.mu + (Delta_v-Delta_tau*self.mu[i])*si
self.iterations += 1
//Sigma recomputation with Cholesky decompositon
self.LLT0 = self.LLT0 + np.dot(self.Kmn*self.tau_tilde[None,:],self.Kmn.T)
self.L = jitchol(self.LLT)
V,info = linalg.flapack.dtrtrs(L,self.Kmn,lower=1)
V2,info = linalg.flapack.dtrtrs(L.T,V,lower=0)
self.Sigma_diag = np.sum(V*V,-2)
Knmv_tilde = np.dot(self.Kmn,self.v_tilde)
self.mu = np.dot(V2.T,Knmv_tilde)
epsilon_np1 = sum((self.tau_tilde-self.np1[-1])**2)/self.N
epsilon_np2 = sum((self.v_tilde-self.np2[-1])**2)/self.N
self.np1.append(self.tau_tilde.copy())
self.np2.append(self.v_tilde.copy())
return self.tau_tilde[:,None], self.v_tilde[:,None], self.Z_hat[:,None], self.tau_[:,None], self.v_[:,None]
class FITC(EP):
def fit_EP(self):
After Change
return self._compute_GP_variables()
class DTC(EP):
def fit_EP(self):
The expectation-propagation algorithm with sparse pseudo-input.
For nomenclature see ... 2013.
Prior approximation parameters:
q(f|X) = int_{df}{N(f|KfuKuu_invu,diag(Kff-Qff)*N(u|0,Kuu)} = N(f|0,Sigma0)
Sigma0 = Qnn = Knm*Kmmi*Kmn
self.Kmmi, self.Kmm_hld = pdinv(self.Kmm)
self.KmnKnm = np.dot(self.Kmn, self.Kmn.T)
self.KmmiKmn = np.dot(self.Kmmi,self.Kmn)
self.Qnn_diag = np.sum(self.Kmn*self.KmmiKmn,-2)
self.LLT0 = self.Kmm.copy()
Posterior approximation: q(f|y) = N(f| mu, Sigma)
Sigma = Diag + P*R.T*R*P.T + K
mu = w + P*gamma
self.mu = np.zeros(self.N)
self.LLT = self.Kmm.copy()
self.Sigma_diag = self.Qnn_diag.copy()
Initial values - Cavity distribution parameters:
q_(g|mu_,sigma2_) = Product{q_i(g|mu_i,sigma2_i)}
sigma_ = 1./tau_
mu_ = v_/tau_
self.tau_ = np.empty(self.N,dtype=float)
self.v_ = np.empty(self.N,dtype=float)
//Initial values - Marginal moments
z = np.empty(self.N,dtype=float)
self.Z_hat = np.empty(self.N,dtype=float)
phi = np.empty(self.N,dtype=float)
mu_hat = np.empty(self.N,dtype=float)
sigma2_hat = np.empty(self.N,dtype=float)
//Approximation
epsilon_np1 = 1
epsilon_np2 = 1
self.iterations = 0
self.np1 = [self.tau_tilde.copy()]
self.np2 = [self.v_tilde.copy()]
while epsilon_np1 > self.epsilon or epsilon_np2 > self.epsilon:
update_order = np.arange(self.N)
random.shuffle(update_order)
for i in update_order:
//Cavity distribution parameters
self.tau_[i] = 1./self.Sigma_diag[i] - self.eta*self.tau_tilde[i]
self.v_[i] = self.mu[i]/self.Sigma_diag[i] - self.eta*self.v_tilde[i]
//Marginal moments
self.Z_hat[i], mu_hat[i], sigma2_hat[i] = self.likelihood.moments_match(i,self.tau_[i],self.v_[i])
//Site parameters update
Delta_tau = self.delta/self.eta*(1./sigma2_hat[i] - 1./self.Sigma_diag[i])
Delta_v = self.delta/self.eta*(mu_hat[i]/sigma2_hat[i] - self.mu[i]/self.Sigma_diag[i])
self.tau_tilde[i] = self.tau_tilde[i] + Delta_tau
self.v_tilde[i] = self.v_tilde[i] + Delta_v
//Posterior distribution parameters update
self.LLT = self.LLT + np.outer(self.Kmn[:,i],self.Kmn[:,i])*Delta_tau
L = jitchol(self.LLT)
V,info = linalg.flapack.dtrtrs(L,self.Kmn,lower=1)
self.Sigma_diag = np.sum(V*V,-2)
si = np.sum(V.T*V[:,i],-1)
self.mu = self.mu + (Delta_v-Delta_tau*self.mu[i])*si
self.iterations += 1
//Sigma recomputation with Cholesky decompositon
self.LLT0 = self.LLT0 + np.dot(self.Kmn*self.tau_tilde[None,:],self.Kmn.T)
self.L = jitchol(self.LLT)
V,info = linalg.flapack.dtrtrs(L,self.Kmn,lower=1)
V2,info = linalg.flapack.dtrtrs(L.T,V,lower=0)
self.Sigma_diag = np.sum(V*V,-2)
Knmv_tilde = np.dot(self.Kmn,self.v_tilde)
self.mu = np.dot(V2.T,Knmv_tilde)
epsilon_np1 = sum((self.tau_tilde-self.np1[-1])**2)/self.N
epsilon_np2 = sum((self.v_tilde-self.np2[-1])**2)/self.N
self.np1.append(self.tau_tilde.copy())
self.np2.append(self.v_tilde.copy())
return self._compute_GP_variables()
class FITC(EP):
def fit_EP(self):
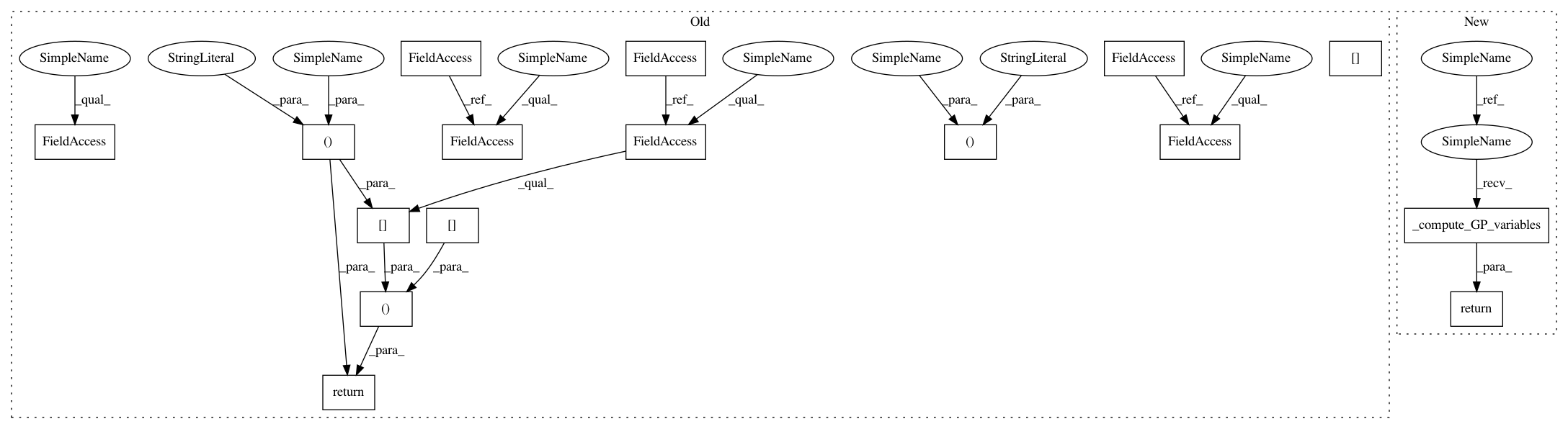
In pattern: SUPERPATTERN
Frequency: 3
Non-data size: 16
Instances
Project Name: SheffieldML/GPy
Commit Name: ec89c4efc300b7e3e5622c6cd018d6fe7deda55b
Time: 2013-01-29
Author: acq11ra@sheffield.ac.uk
File Name: GPy/inference/EP.py
Class Name: DTC
Method Name: fit_EP
Project Name: SheffieldML/GPy
Commit Name: ec89c4efc300b7e3e5622c6cd018d6fe7deda55b
Time: 2013-01-29
Author: acq11ra@sheffield.ac.uk
File Name: GPy/inference/EP.py
Class Name: Full
Method Name: fit_EP
Project Name: SheffieldML/GPy
Commit Name: ec89c4efc300b7e3e5622c6cd018d6fe7deda55b
Time: 2013-01-29
Author: acq11ra@sheffield.ac.uk
File Name: GPy/inference/EP.py
Class Name: DTC
Method Name: fit_EP
Project Name: SheffieldML/GPy
Commit Name: ec89c4efc300b7e3e5622c6cd018d6fe7deda55b
Time: 2013-01-29
Author: acq11ra@sheffield.ac.uk
File Name: GPy/inference/EP.py
Class Name: FITC
Method Name: fit_EP
