ba1182eeaaadb1805319166022128f4823f491f9,tslearn/docs/examples/plot_barycenters.py,,,#,19
Before Change
plt.figure()
plt.subplot(2, 1, 1)
for ts in X:
plt.plot(numpy.arange(sz), ts, "k-", alpha=.2)
plt.plot(numpy.arange(sz), EuclideanBarycenter().fit(X), "r-", linewidth=2)
plt.title("Euclidean barycenter")
After Change
sdtw = SoftDTWBarycenter(gamma=1., max_iter=100)
sdtw_bar = sdtw.fit(X)
for ts in X:
plt.plot(ts.ravel(), "k-", alpha=.2)
plt.plot(sdtw_bar.ravel(), "r-", linewidth=2)
plt.title("Soft-DTW barycenter ($\gamma$=1.)")
plt.tight_layout()
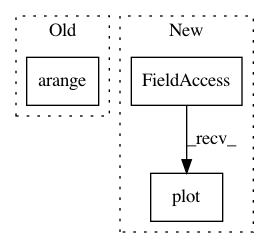
In pattern: SUPERPATTERN
Frequency: 3
Non-data size: 3
Instances
Project Name: rtavenar/tslearn
Commit Name: ba1182eeaaadb1805319166022128f4823f491f9
Time: 2017-06-22
Author: romain.tavenard@univ-rennes2.fr
File Name: tslearn/docs/examples/plot_barycenters.py
Class Name:
Method Name:
Project Name: rtavenar/tslearn
Commit Name: ba1182eeaaadb1805319166022128f4823f491f9
Time: 2017-06-22
Author: romain.tavenard@univ-rennes2.fr
File Name: tslearn/docs/examples/plot_kmeans.py
Class Name:
Method Name:
Project Name: rtavenar/tslearn
Commit Name: 495d64386cb00b6be050475bbff545e0a0115e94
Time: 2020-03-27
Author: johann.faouzi@gmail.com
File Name: tslearn/docs/examples/plot_lb_keogh.py
Class Name:
Method Name:
