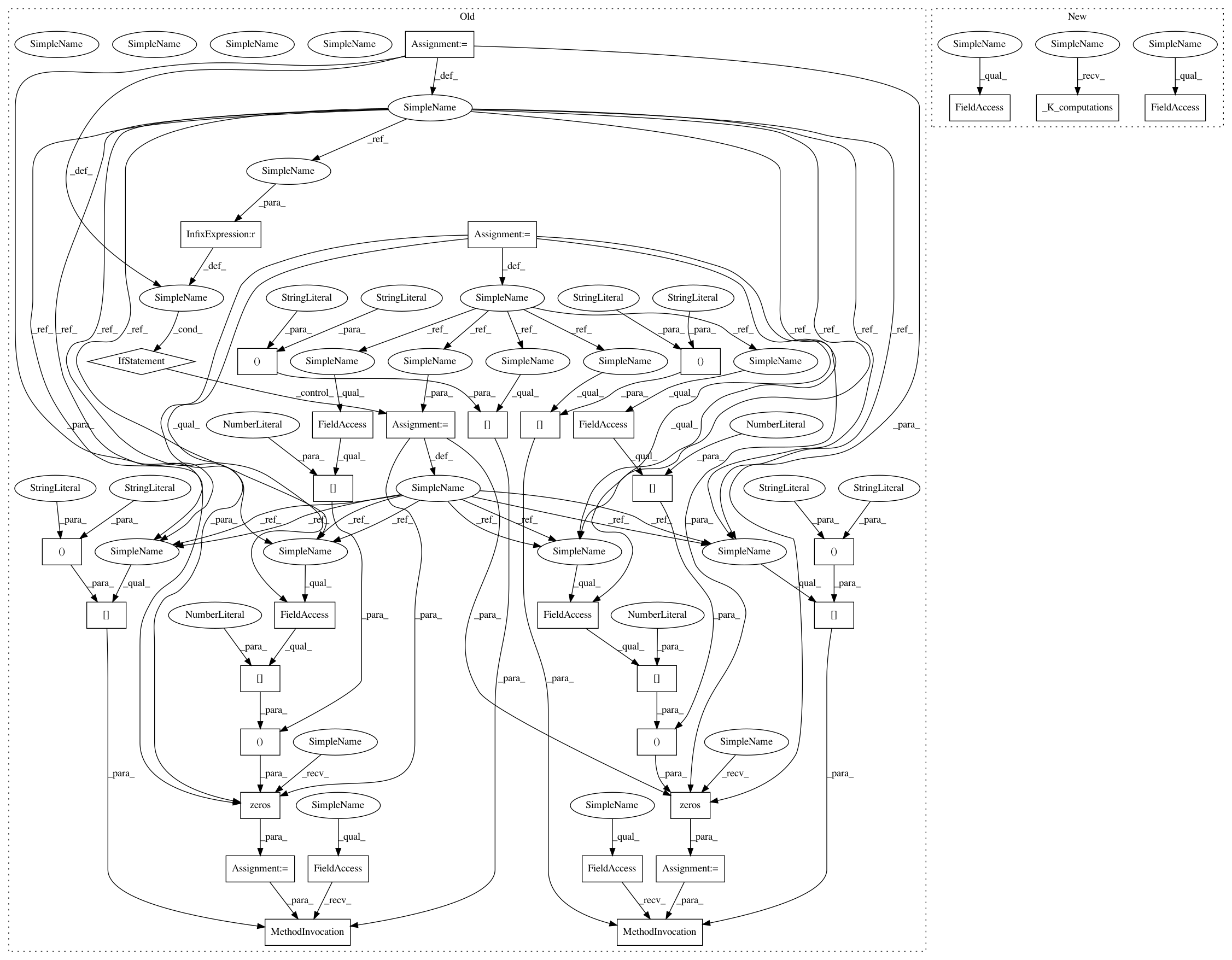
f35578804a2dcbc9066d48a103bcaf4ed1d0fd5d,GPy/kern/prod_orthogonal.py,prod_orthogonal,dK_dX,#prod_orthogonal#Any#Any#Any#Any#,76

Before Change

    def dK_dX(self,dL_dK,X,X2,target):
        derivative of the covariance matrix with respect to X.
        if X2 is None: X2 = X
        K1 = np.zeros((X.shape[0],X2.shape[0]))
        K2 = np.zeros((X.shape[0],X2.shape[0]))
        self.k1.K(X[:,0:self.k1.D],X2[:,0:self.k1.D],K1)
        self.k2.K(X[:,self.k1.D:],X2[:,self.k1.D:],K2)

        self.k1.dK_dX(dL_dK*K2, X[:,:self.k1.D], X2[:,:self.k1.D], target)
        self.k2.dK_dX(dL_dK*K1, X[:,self.k1.D:], X2[:,self.k1.D:], target)

After Change

    def dK_dX(self,dL_dK,X,X2,target):
        derivative of the covariance matrix with respect to X.
        self._K_computations(X,X2)
        self.k1.dK_dX(dL_dK*self._K2, X[:,:self.k1.D], X2[:,:self.k1.D], target)
        self.k2.dK_dX(dL_dK*self._K1, X[:,self.k1.D:], X2[:,self.k1.D:], target)

    def Kdiag(self,X,target):
        Compute the diagonal of the covariance matrix associated to X.

Instances